
Sometimes two games are the same even if they look completely different. An example involves the game of noughts and crosses and another game called Fifteen.
Most people are familiar with noughts and crosses. It's played on a grid of nine squares. Players take turns in marking squares with their symbol, which is a cross for one player and a 0 for the other. The winner is the first person who manages to mark three squares in a line, either vertically, horizontally or diagonally.
Fifteen involves the numbers 1 up to 9. In this game, players take turns to pick one of the numbers. They can only pick numbers that haven't been picked before. The winner is the first person to pick three numbers that add up to 15.
What's the similarity? Both games involve the number 9: there are nine squares in noughts and crosses and nine numbers in fifteen. This suggests writing the numbers 1 to 9 into the squares of a noughts and crosses game. Once you have done that, when a player marks a square he or she automatically picks a number at the same time (the number that is in the square). So with the numbers entered into the squares, a game of noughts and crosses is also a game of Fifteen at the same time.
But what about winning the games? A player wins noughts and crosses if they manage to mark three squares in a line. If the same player is also to win the corresponding game of Fifteen, we can't fill the numbers into the squares in any old way. What can you say about the way the nine numbers need to be arranged in the grid?
They have to be arranged so that the numbers in each row, column and diagonal of the grid add to 15.
Can you figure out where in the grid to write each number from 1 to 9 to make sure the player who wins noughts and crosses also wins Fifteen?
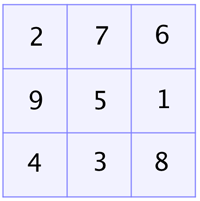
You can now see that a game of noughts and crosses can be translated exactly into a game of Fifteen. The first player marking a particular square corresponds to the first player picking the corresponding number in fifteen. The second player marking one of the remaining squares corresponds to the second player in Fifteen picking one of the remaining numbers. And so on. And because of the way we have written the numbers in the squares, we know that the player who wins noughts and crosses also wins Fifteen. The same works the other way around, as you can check for yourself. A game of Fifteen can be translated exactly into a game of noughts and crosses.
When two games are equivalent in this way, when one game can be translated exactly into the other, we say that they are isomorphic. There are several pairs of games on this site that are isomorphic. Can you find them?

Comments
wow
This was something I can learn from. Some parts easy, some parts hard. But wow, so fun!!!!!