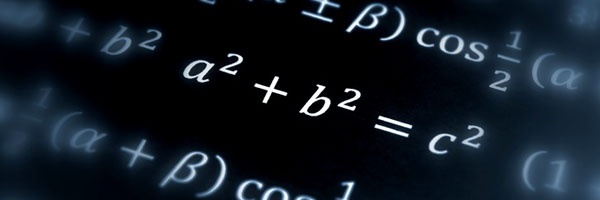
"I think I'll stop here." This is how, on 23rd of June 1993, Andrew Wiles ended his series of lectures at the Isaac Newton Institute in Cambridge. The applause, so witnesses report, was thunderous: Wiles had just delivered a proof of a result that had haunted mathematicians for over 350 years: Fermat's last theorem.
The theorem is linked to maths that is over 2000 years old. Most people have heard of Pythagoras' theorem: if $a$, $b$ and $c$ are the sides of a right-angled triangle, with $c$ the side opposite the right angle, then $$a^2+b^2=c^2.$$ There are infinitely many triples $a$, $b$ and $c$ of natural numbers which satisfy this equation. Examples are $(3,4,5)$, $(5,12,13)$ and $(6,8,10).$ They are called Pythagorean triples.
Fermat's last theorem looks at similar equations but with different exponents. Are there triples of natural numbers that satisfy $$a^3+b^3=c^3,$$ or $$a^4+b^4=c^4,$$ or $$a^5+b^5=c^5?$$ More generally, can we find triples of natural numbers that satisfy $$a^n+b^n=c^n,$$ where $n$ is any natural number? The 17th century mathematician Pierre de Fermat convinced himself that such triples don't exist for any natural number $n>2$. In 1637 he wrote into the margin of his maths textbook that he had found a "marvellous proof" for this fact, which the margin was too narrow to contain. That tantalising scribble was to taunt mathematicians for a long time.
Watch Andrew Wiles talk about what it feels like to do maths.
When Wiles announced his proof at the Newton Institute he had spent seven years working on the problem in secret, avoiding the attention he would have attracted had he admitted to what he was doing. In fact he had been working on a more general problem, called the Taniyama-Shimura conjecture, whose solution implied Fermat's last theorem, but which was considered pretty inaccessible by most mathematicians at the time. "But Although Wiles hadn't published anything on this topic, everyone knew if anyone was to prove Fermat's last theorem, he had a good chance," recalls Tom Körner, a mathematician at the University of Cambridge. "I had interviewed Wiles for a fellowship at Trinity Hall, Cambridge, just before he moved to Princeton. Everyone said he was brilliant."
Before Wiles announced his proof he had already lectured for two days, as part of a research programme at the Newton Institute. "Rumours were flying around that something important would happen on the third day," says Körner. "I asked his student what was happening and he said 'I can't tell you'. I asked him 'Will I regret not being there on the last day?' and he said 'Yes'."
Wiles' lecture lived up to expectations: "The atmosphere was electric," says Körner. "After he finished, there was a storm of applause and then the few people in the audience who knew the material asked questions, and then said the result looked good."
And it is not all about the bottom line. "Wiles' proof has had a greater impact than that of other results, like the four colour theorem, because of the mathematics that was created to prove the theorem," says Körner. As it turned out, Wiles' proof did contain a flaw which took another year and help from a former student, Richard Taylor, to fix. But in the end the 357-year-old-problem yielded to the sophisticated techniques developed to crack it.
Further reading
You can find out more in the Plus magazine article Fermat's last theorem and Andrew Wiles.
