When you look at a map, you usually find that countries are coloured in different colours. To avoid confusion, neighbouring countries obviously shouldn't have the same colour. So, given any map drawn on a flat piece of paper, how many different colours will you need to colour it? Map makers have know for centuries that the answer is always at most four. As you'll soon find after playing around with a few maps, no matter how complicated they are, you can always colour them with only four colours. Try it for yourself!

This "map" is quite fanciful, but you still only need four colours to colour it. Image: Inductiveload, CC BY-SA 3.0.
Now only because nobody has as yet found a map that needs more than four colours, doesn't mean that such a map doesn't exist — and this is what makes this fact interesting to mathematicians. Is it possible to prove that no map drawn on a piece of paper needs more than four colours? Mathematicians have tried for a long time, but have found the task surprisingly difficult. The first proof was published in 1879, but was found to contain a flaw eleven years later.
It wasn't until nearly a hundred years later, in 1976, that a correct proof was published and it was a proof that rocked the world of mathematics. The mathematicians Kenneth Appel and Wolfgang Haken attacked the four colour problem using a proof by contradiction. The idea behind this is quite simple: if a particular assumption leads you to a contradiction, then you know that the assumption must be false. You can think of in terms of investigating a murder case. If the assumption that the gardener committed the murder leads you to conclude that the gardener was in two places at once, which is a non-sensical contradiction, then clearly the assumption is false and the gardener is innocent.
In the same spirit, Appel and Haken assumed that there are maps that need more than four colours to be coloured. If these maps exist, then pick the one that has the smallest number of countries, called the "minimal criminal" for obvious reasons. Appel and Haken showed that the minimal criminal must contain one of 1,936 possible configurations. They also proved that every one of these possible configurations can be reduced into a smaller configuration which also needs more than four colours. This is a contradiction because we assumed that we already started with the smallest five-colour map. Therefore, the original assumption — that there are maps that need more than four colours — must have been false.
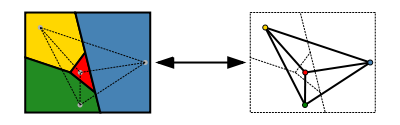
The proof involved turning the map into a graph, with each country represented by a vertex, and two vertices linked if the corresponding countries are neighbours. Colouring a map so that neighbouring countries have different colours corresponds to colouring a network so that linked vertices have different colours. Image: Inductiveload, CC BY-SA 3.0.
What made this proof so outrageous was the fact that part of it was done by a computer. The computer simply ploughed through every one of the 1,936 configurations and checked it. The proof, if printed out by the computer, would take endless amounts of paper: no human being could in their lifetime ever actually read the entire proof to check that it was correct. Several mathematicians of the time complained that this meant that it wasn't really a proof at all! If nobody could check the proof, how could we ever know whether it was right or wrong? So not everybody was convinced that the four-colour theorem had really been proved.
More recently, in 1996, Neil Robertson, Daniel Sanders, Paul Seymour and Robin Thomas came up with a simpler proof involving only 633 configurations. It still needed a computer, but in 2005 the proof was verified using special software developed to process mathematical proofs. To most mathematicians, this removed the last doubt as to whether the proof is valid.
You can find out more about computer proofs in the (slightly more advanced) articles Welcome to the maths lab and The future of proof on Plus magazine.
