
Once you start looking out for graphs, you will find that they appear all over the place. Transport networks are graphs, and so are friendship networks, or social media networks. But that's not all – graphs can also help solve problems that at first sight don't involve any graphs at all.
Many of these problems involve graph colourings. These are ways of colouring the vertices (or edges) of a graph so that two vertices that are linked (or edges that are attached to the same vertex) have different colours.
As an example, imagine that your school needs to schedule eight exams. The exams can't all take place at the same time because some students need to take several of them, and those students obviously can't be in two places at once. How many time slots do you need for scheduling the exams in order to avoid clashes?
To answer this question, draw a graph that has the exams as its vertices, with two vertices being linked by an edge if the corresponding exams can't take place at the same time. Here is an example:
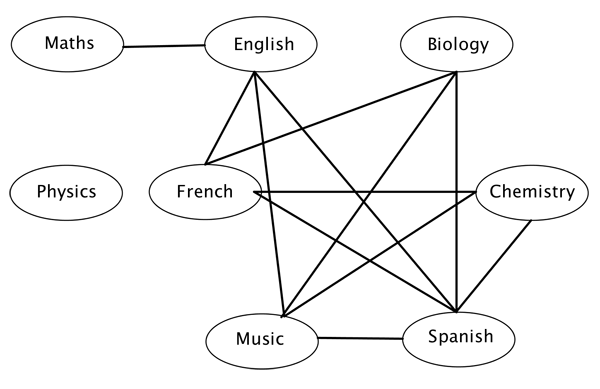
Now find a colouring of the vertices so that no two vertices that are linked have the same colour. You could start by finding a triangle within the graph. Since each vertex in the triangle is linked to the other two, you clearly need three colours to colour them. Let's pick red, blue and green:
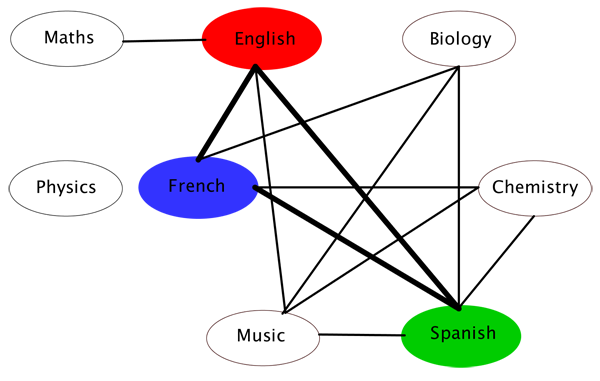
Because it is linked to the red and green vertices in our triangle, the music exam vertex must be blue:
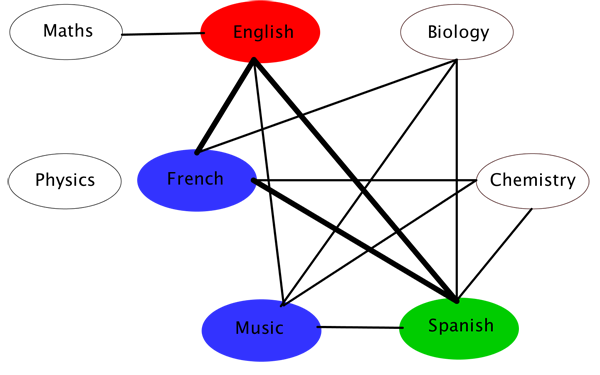
The biology and chemistry exam vertices must now be red:
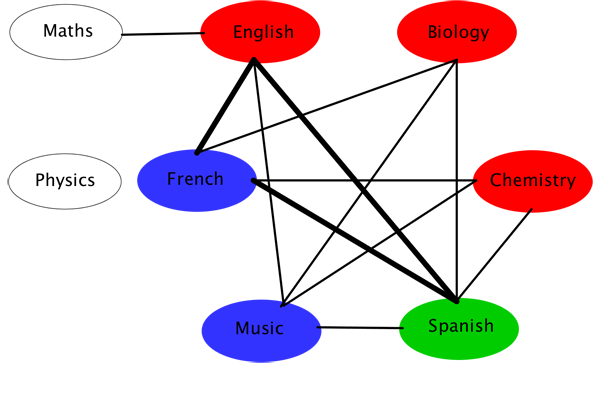
For the remaining two vertices there's a choice of colours — let's pick blue:
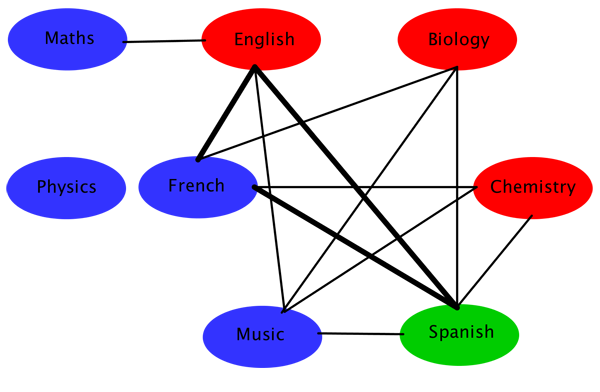
It turns out that we needed three colours to colour the vertices of our graph. Since no two connected vertices have the same colour, and vertices are connected if the corresponding exams can't take place at the same time, we know that we need as many time slots to schedule the exams as there are colours: three. Here is a possible schedule:
| Monday | Tuesday | Wednesday |
| English | Maths | Spanish |
| Biology | Physics | |
| Chemistry | French | |
| Music |
There are many other scheduling and allocation tasks that can be solved using graph colourings. For example, airlines need to allocate their aircraft to flights so that no aircraft is required to be in two places at once, sports organisations need to schedule sporting events, such as tennis tournaments, so that the matches of the individual players don't clash, and mobile phone companies need to assign frequencies to mobile phone transmitters in such a way that nearby transmitters don't interfere with each other. The list of applications of graph colourings is very long indeed!
To find out how graph colouring is related to one of the most famous problems in mathematical history, see Four is Fine.
