
You may find it useful to have paper, ruler, compasses and scissors to try this task.
How could you work out the area of a regular dodecagon?
One way to find the area of shapes is to cut them up and reassemble them into shapes where the area is easier to calculate.
Start by creating your dodecagon. You could use GeoGebra or construct it with a ruler and compasses.
Click below to see some instructions for constructing a dodecagon, or watch the video.
Keeping your compasses at the same separation, mark off six points around the circle.
Bisect one of the six arcs, and then use this distance to mark off the remaining six points.
Next, construct an equilateral triangle inside each edge of the dodecagon, and join points to make the following diagram:
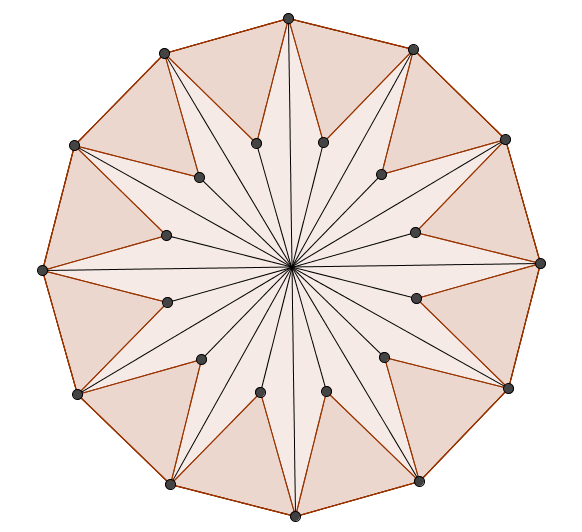
By cutting out and rearranging some of the pieces, can you create a shape made up of squares?
If you want to see how to construct the triangles and rearrange the pieces, take a look at the video below:
Can you use this dodecagon dissection to prove that the area of a regular dodecagon is $3r^2$, where $r$ is the radius of the circle passing through the vertices?
