
We can imagine that a squirrel has four favourite trees, from 1st to 4th.
The squirrel heads towards the 1st tree but stops half-way (he finds a nut and buries it!). He changes direction and heads towards the 2nd tree but half-way he finds a nut (as before he buries it!). He then heads towards the 3rd tree and stops half-way etc. After heading towards the 4th he heads towards the 1st tree and keeps going in the same way.
These diagrams may help. . .
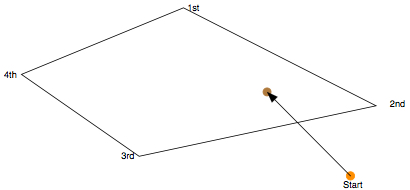 then
then 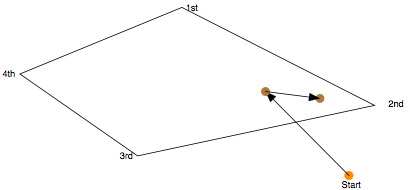 then
then 
The third diagram shows the squirrel heading towards the 4th , and that's as far as the diagrams go.
So explore by continuing past the 4th to head towards the 1st again and so on.
Comments
possible solution
After the said squirrel reaches half way to the fourth tree (if we were to imagine its path restarted and when it continues) by going half way to each tree, it would create a quadrilateral, a kite. This is also the same as the shape made if the said squirrel was to go to each tree, starting with the 1st tree. If the squirrel was to continue until it would reach a tree, it will keep on going for ever.
- Log in to post comments
