
You will need a 5 by 5 square and a dice.
Place your dice in the top left hand corner.
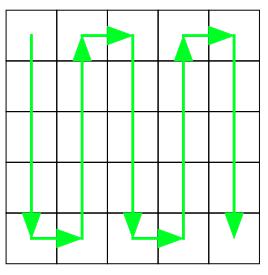
Whatever number is on the top of the dice, write it down on the square.
Follow the green line on this grid as a route by rolling your dice, writing down the numbers on top of the dice as you move along. You can see in this video how it might be started. Have a good look at what's happening and then carry it on in a similar way.
When you've filled all 25 squares with numbers, EXPLORE!
What do you notice?
Comments
Roll dice
What fun we had! The number patterns are repeated no matter how many squares your grid has so once we recognised the pattern, we could complete the rest of the square without having to roll the dice! There were always lines that were exactly the same numbers going vertically if you moved the dice from side to side & horizontally if you moved the dice up & down. When we experimented with an even number of squares, there was still a pattern although not so obvious. However with the odd number squares you can add more squares on the end & below as the pattern is self-explanatory but with the even squares, you can only continue the pattern in the direction you are already going.
- Log in to post comments
roll over the dice
I had so much fun rolling the dice! I discovered the second and fourth row turned out with the same figures. The second row was Number 6 which rolled up across the column grid. The fourth row was Number 1.... I experimented with all the numbers on the dice. Next time, i will roll over in even and odd number patterns.
- Log in to post comments
Berkhamsted Prep School
We found the following:
- The number patterns are repeated. These are the first 20 numbers in the first 4 rows.
- The second and fourth row turned out with the same figures.
- All 4 corners had the same number.
- The diagonals had the same total.
- The 2 digits that have a whole row are not found anywhere else on the grid.
- Log in to post comments
this
its cool, there was numbers in the 2nd and 4th row there is the same numbers in a line.
- Log in to post comments
maths
really good stuff, keep being fresh and epic. peace. $vince$
- Log in to post comments
really fun and made us
really fun and made us explore!!!
- Log in to post comments
fun and enjoyable!!
fun and enjoyable!!
- Log in to post comments
hi
reallt good activity kaka
- Log in to post comments
Investigation
We had a great time
- Log in to post comments
The magic number is 84
The total of all the numbers in the grid is 84 plus whatever you strated with.
- Log in to post comments
The dice problem!!!!!!!!!!!!!
All the columns and rows start and finish with the same numbers and all the even rows have the same number all the way along!!!!!!!!!!!!!!!!!!!!!!!!!!
My 1's are all in a triangle,my 4's are in a x,my 2's and 5's are in a horizontal line and my 3's are in a diamond !
- Log in to post comments
the dice thing
i found that mine was a repeating pattern
- Log in to post comments
New challenge
Why not add up all your dice numbers you got at the end?
- Log in to post comments
a pattern
I have noticed that the pattern 6,5,1,2 appears on the first line, the last line, the first column and the last column.
I also found that the pattern was repeating itself: 6, 5, 1, 2.
- Log in to post comments
The Opposites
In our case we found that:
*The first row and colum is identical to the fifth one.
*We also found that in the second line we found repeated six and in the fourth line repeated one.
*In the corners there are five.
*Our starting number was 5.
- Log in to post comments
more odd than even
when I did it I got 17 odd numbers and 10 even numbers I think this happened because I started with a even number so when you turn corners, it goes to odd numbers. That's why I think there are more odd numbers than even numbers.
- Log in to post comments
At our enriching lunch club
At our enriching lunch club today we discovered that this is an awesome investigation which has many patterns to discover. When we discovered the corners were the same, two rows were the same, diagonals, and middle of each edge the same we tested our theory by checking each others’ predictions. It was awesome and fun!!!!
Max, Joe, Aidan, Joshua and Jacob
New Hall School pupils – ‘the best school in the world’
- Log in to post comments
