
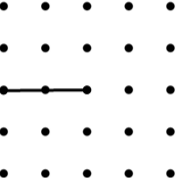
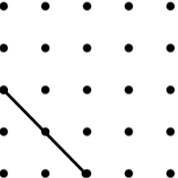
Join dots on each grid below to make the named quadrilateral.
You must use the side given, you can't shorten or extend it.
If there is more than one possibility, try to find the one with the largest area.
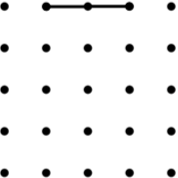
| 1 Rectangle |
2 Square |
3 Rectangle |
 |
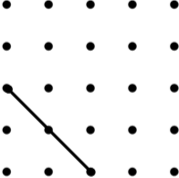 |
 |
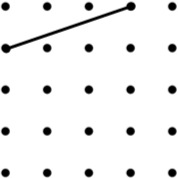
4 Isosceles Trapezium |
5 Parallelogram |
6 Kite |
 |
 |
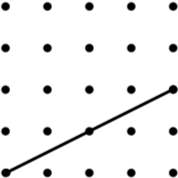 |
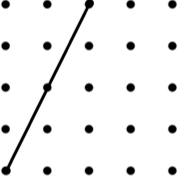
7 Parallelogram |
8 Square |
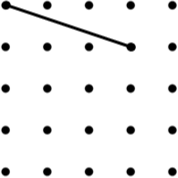
9 Kite |
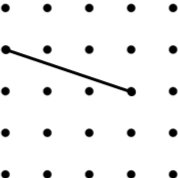 |
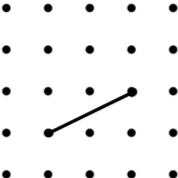 |
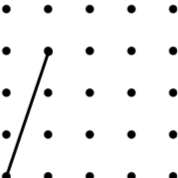 |
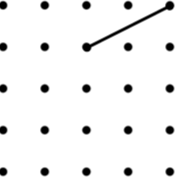
10 Rhombus |
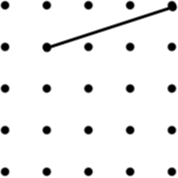
11 Parallelogram | 12 Kite |
 |
 |
 |
13 Arrowhead |
14 Kite | 15 Rhombus |
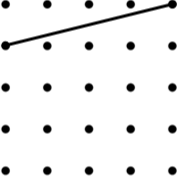 |
 |
 |
16 Rhombus |
17 Arrowhead | 18 Trapezium |
 |
 |
 |
19 Parallelogram |
20 Isosceles Trapezium | 21 Kite |
 |
 |
 |
22 Arrowhead |
23 Kite | 24 Trapezium |
 |
 |
 |
You may find it useful to print this worksheet of the problem.
Once you've completed the quadrilaterals, here are some questions you might like to explore:
How many different squares is it possible to draw on a $5$ by $5$ grid like the ones above?
How many different rhombuses is it possible to draw on a $5$ by $5$ grid like the ones above?
Or parallelograms, or trapezia, or...
What about grids of other sizes?
With thanks to Don Steward, whose ideas formed the basis of this problem.
