
Charlie has been thinking about which numbers can be written as a sum of square numbers.
He took a $10\times10$ grid, and shaded all the square numbers in blue.
He then shaded the numbers that were the sum of two squares in yellow.
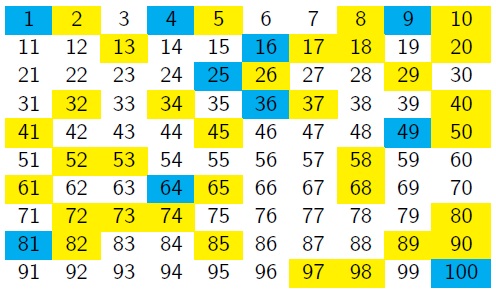
He hoped to find a pattern, but couldn't see anything obvious...
Vicky suggested changing the number of columns in the grid, so they reduced it by one:
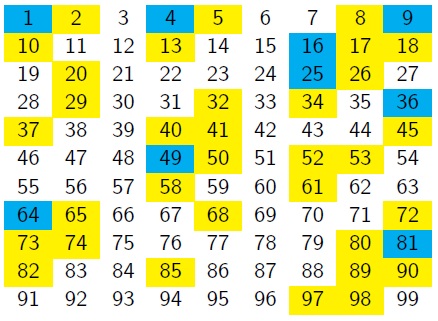
Can you spot any patterns?
Can you explain them?
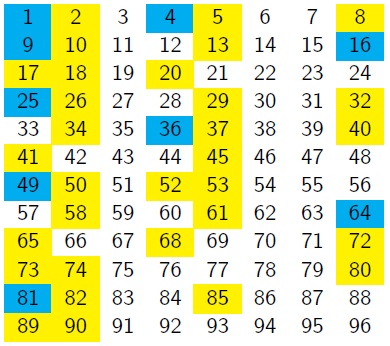
What do you notice?
Can you make any conjectures about the columns in which squares, and sums of two squares, would appear if the grid continued?
Can you prove any of your conjectures?
What happens if you also colour in the numbers which are sums of three square numbers? Where are the gaps now?
It's possible to write ANY whole number as the sum of four square numbers, but this is hard to prove - it was first proved in 1770 by Lagrange.
