Fold and Cut | wild.maths.org

Diamond Challenge

What do you 'see' when you think of the word 'diamond'?

Can you make a suit of diamonds (the playing card sort!) using only a rectangle of paper for each new card, folded as many times as you like and cut once, to create diamonds holes, before opening out?

Share your thoughts and discoveries

Snowflakes

Snowflakes, famously, are six-sided and they also have six-fold symmetry. Here's some photographs of snowflakes with six-fold symmetry made from a single square sheet of paper (12 cm by 12 cm) by folding and cutting:

Toolbox

Do you know what each diamond playing card looks like?

There are a few below to get you thinking about what the other designs might look like…

Try drawing some lines of symmetry on them.

What might these have to do with the task?

Start Simple

Start with the Ace card…

Draw the single diamond shape in the centre of a piece of paper.

Try folding along the lines of symmetry and then think about where you could cut just once to create a hole where your diamond was.

Work systematically…

Which cards might you move on to after working out how to make the Ace?

Perhaps looking at some of my mistakes will help you to think about ways you could improve on them?

Dig Deeper

You might like to try the NRICH problem called Folding, Cutting and Punching.

Or can you reason which of the following punched pictures could have been made from the instructions above it?

Snowflake Toolbox

Watch how to make a six-fold paper template to cut the snowflake:

Watch how to cut the snowflake from the six-fold paper template:

Snowflake Start Simple

Start with a rectangular piece of paper. Fold it in half and half again.

How could you make just one straight cut to create a square?

What other shapes could you make by folding a rectangular piece of paper and making just one cut?

Snowflake Library

If you'd like to read more about the symmetry of snowflakes, try this article written by Ian Stewart, Emeritus Professor of Mathematics and Digital Media Fellow at Warwick University.

Did you know that the world's largest ever snowflake found (to date) was 38 centimetres wide and 20 centimetres thick? Find more snowflake facts in the library.

Or perhaps you're more interested in snow facts? How tall do you think the world's tallest snowman is, for example?

Snowflake Dig Deeper

Koch Snowflake Fractals

A.Interesting facts

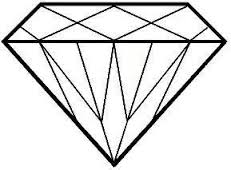
The Koch snowflake is sometimes called the Koch star or the Koch island.
It was discovered by the Swedish mathematician Helge Von Koch in 1904.
It is a continuous curve that does not have a tangent at any point.
The rule for generating the Koch snowflake: start with an equilateral triangle. Replace each line segment by a zig-zag curve (a generator) made up of four copies of the line segment it replaces, each reduced to one third of the original length. Repeat the same process for every line segment of the new shape, and keep repeating forever, for each new shape in turn. One can imagine doing this yet it is the maths that helps us to go on ad infinitum.
Its perimeter is infinite yet its area is finite.
It is a member of the fractal family.

B. Find out more about fractals.

Fractals are geometric objects that exhibit complex structure at every scale. No matter how closely you zoom in on a fractal, its complexity doesn't diminish and you often see the same structures appearing again and again. A famous example is the Von Koch snowflake. Start with an equilateral triangle and replace the middle third of each side by a "spike" consisting of two sides of a smaller equilateral triangle. Now do the same for each of the twelve straight-line segments of the resulting shape and repeat, ad infinitum. The shape you get in the end, after an infinite number of steps, exhibits the same spiky structure at every level of magnification: you'll never see a piece of straight line in its outline, because every straight-line piece that was once there has been broken up and adorned with a spike.

Mathematically, fractals live in a strange world in between dimensions. You couldn't call the Von Koch snowflake "one-dimensional" because it contains no straight lines or smooth curves at all. No amount of zooming in will reveal such one-dimensional components. On the other hand, the snowflake isn't two-dimensional either, because it occupies no area. In fact, it takes a new definition of "dimension" to sort out the snowflake's place in the dimensional hierarchy. According to this definition, the snowflake has a dimension of around 1.26. Having a fractional dimension, one that's not a whole number, is what characterises the objects Mandelbrot decided to call fractals.

D. Things to do

Try constructing one using the computer programme Scratch.
Try investigating the perimeter as the snowflake grows.
Try the squareflake for a bit of variety.