How far is it from your house to your school? The obvious way of answering this question is to get a map out and measure the straight line from your house to school: from my house to school this distance is 1471 metres. This straight-line distance between two locations on a map is often called "as the crow flies". But unfortunately I can't fly and instead have to go by road, either walking or cycling. By road, the shortest distance from my house to school is 1994 metres.
The other way I think about how far it is, is how long it takes me to get there: walking takes 25 minutes and cycling 8 minutes, even though they are both along the same route. How you move between the two points has a great effect on the distance you measure.
We can see that our familiar notion of distance, the length of a straight line between two points (as the crow flies), is not the only way to measure distance. In maths, a rule for how to measure distance is called a metric, and there can be many different metrics for measuring distance over the same space. A metric takes two points and gives a real number for the distance between them (as measured by that particular metric) .
The rules a metric has to satisfy are fairly obvious. It has to be symmetric: that is the distance it gives from home to school should be the same as the distance from school to home. The second rule is that the distance between two points is zero if they are located in the same place, and vice versa. And finally, the metric has to satisfy the triangle inequality: that the distance as measured on two sides of a triangle is always greater than or equal to the distance as measured along the third side.
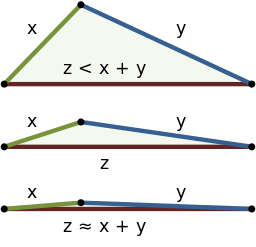
The triangle inequality: the sum of the lengths of two sides of a triangle exceeds the length of the third side. (Image by By WhiteTimberwolf, Brews ohare – CC BY-SA 3.0)
Metrics are an important tool in mathematics, and they also have important applications in physics and in everyday life. For example the distance measured on the two-dimensional surface of a sphere (spherical geometry) is different to that measured on a flat piece of paper. This is why the routes flown by planes (which follow the great circles, the shortest distances around the roughly spherical earth) look like curves on a flat map of the earth. And of course, this spherical distance is not the same as the shortest distance you'd measure in three dimensions, which would be a straight line passing through the inside of the sphere.
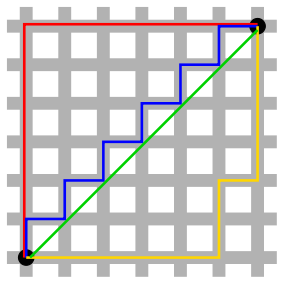
Metrics also come from real world examples, such as the British Rail metric where the distance between two points is the sum of their distances to London (as most train journeys used to go via London), unless they lie on the same train line. And some of these have interesting mathematical uses. For example, the taxicab metric comes from the grid layout of the streets in Manhattan, USA – it's also known as the Manhatten distance. The taxicab metric mimics this by measuring the distance between two points along a route between them on a square grid. The taxicab metric is in fact the same as something called the Hamming distance, an important concept from coding theory and digital communications.