
Here is a diagram showing how vectors can be used to describe a journey round a square:
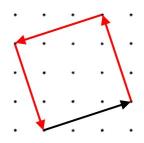
The journey starts along the black vector $\pmatrix{3\cr 1}$
Which vectors describe the rest of the journey?
Draw some vector journeys around squares of your own and see what you can find out. You may wish to print out some dotty paper.
Here are some questions you might like to consider:
What happens if I add vectors together?
What is special about opposite sides of the squares?
What is special about adjacent sides of the squares?
If I know the vector for the diagonal can I work out the other vectors?
What about other shapes?
