
Choose four consecutive whole numbers.
Multiply the first and last numbers together.
Multiply the middle pair together.
Choose several different sets of four consecutive whole numbers and do the same.
What do you notice?
Can you explain what you have noticed? Will it always happen?
Click below to see how Charlie and Alison explained what they noticed.
Charlie said:
I can explain this by labelling the four consecutive numbers $n, n+1, n+2, n+3$.
Outer pair: $n(n+3) = n^2 + 3n$
Inner pair: $(n+1)(n+2) = n^2 + 3n + 2$
Alison said:
I drew a diagram, in which the product of each pair is represented by the area of a rectangle
The outer pair is represented by the red rectangle.
The inner pair is represented by the blue rectangle.
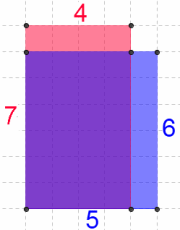
The purple area is common to both.
The area of the red strip will always be two units less than the area of the blue strip.
Therefore, the product of the outer pair is always two less than the product of the inner pair.
Charlie used his representation to explore what happened when he had more than four consecutive numbers...
Alison used her representation to explore what happened when she had sets of numbers that went up in threes...
You may wish to explore Charlie's and Alison's ideas or come up with some questions of your own.
Can you explain any results that you discover?
Comments
we can represent the four
We can represent the four numbers as n, n+1, n+2 and n+3...
The outer pair would be $n(n+3) = n^2 + 3n$
Inner pair: $(n+1)(n+2) = n^2 + 3n + 2$
Therefore there would always be a diference of 2 (The inner pair being bigger)
- Log in to post comments
we can represent the four
Can you use similar reasoning to explain what will happen when you compare the product of the first and last numbers with the product of the second and penultimate numbers, when you have more than four consecutive numbers?
- Log in to post comments
