
How do you win a game of Nim? In this article we'll explore the winning strategy— but it's not for the mathematically faint-hearted!
The rules of Nim
The traditional game of Nim is played with a number of counters arranged in heaps: the number of counters and heaps is up to you. There are two players. When it's a player's move he or she can take any number of coins from a single heap. They have to take at least one coin, though, and they can't take coins from more than one heap. The winner is the player who makes the last move, so there are no coins left after that move.
As an example of how the game works, suppose there are three heaps with three, four and five coins respectively. Here is how the game could develop (the two players are called A and B):
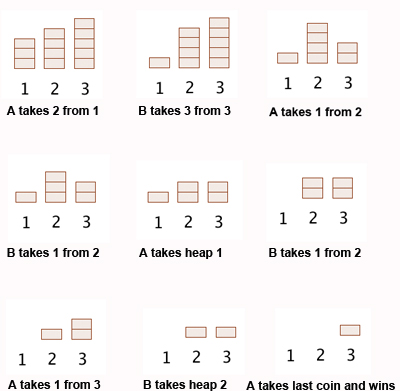
The question we're interested in is this: given a particular configuration of heaps and coins, is there a winning strategy for one of the players? That is; is one of the players guaranteed to win if he or she plays the right moves?
Let's start by playing with some examples. Suppose that player A goes first. Suppose there are two heaps with a coin each. Then clearly, player B is guaranteed to win: A has to take one of the two coins, leaving B to take the last one.
Now suppose that there are two heaps, one of which contains two coins and the other one. Now player A has a winning strategy: take one of the coins in the two-coin heap. This leaves two heaps with a coin each and B to go next. And as we saw in the previous example, this means that A will win.
Let's do one more: suppose that there are two heaps with two coins each. Now player B has a winning strategy. If A takes an entire heap, then B should take the remaining heap and win. If A takes only one coin of one of the heaps, then we are in the same situation as in the previous example, with B to go first. Therefore, B is guaranteed to win if she takes one coin from the two-coin heap.
When you play a few more games of Nim you can't help but feel that there is some sort of pattern here: that there should be some sort of clever trick that tells you for a given arrangement of coins and heaps whether there is a winning strategy for one of the players. The American mathematician Charles Bouton (1869-1922) felt the same and set himself the daunting task of analysing the game completely. In 1902 he found the trick — and it's subtle! To figure out whether there is a winning strategy and for which player, you need to...
Add the Nim way
The secret to finding the winning strategy is to first count the number of counters in each heap and to write that number in binary (see here for an explanation). You then add the binary numbers giving all the different heap sizes — but not using the ordinary way of adding numbers, but something appropriately called Nim addition.
To add some given binary numbers using Nim addition, you first write them underneath each other, as you might for ordinary addition. Then you look at each of the columns in turn. If the number of 1s in a column is odd, you write a 1 underneath it; if it's even, you write a 0 underneath it. Doing this for each column gives a new binary number, and that's the result of the Nim addition.
As an example, let's Nim-add the binary numbers 10, 11, and 100 (which stand for the decimal numbers 2, 3 and 4):
| 1 | 0 | ||
| 1 | 1 | ||
| 1 | 0 | 0 | |
|
|
|||
| 1 | 0 | 1 | |
So the result, which is called the Nim sum, is the binary number 101. Nim addition is not the same as ordinary addition: the binary number 101 is 5 in decimal, which is not equal to the ordinary sum 2+3+4 = 9.
Who wins?
When Charles Bouton analysed the game of Nim, he figured out two facts which hold the key to the winning strategy.
Fact 1: Suppose it's your turn and the Nim sum of the number of coins in the heaps is equal to 0. Then whatever you do, the Nim sum of the number of coins after your move will not be equal to 0.
Fact 2: Suppose it's your turn and the Nim sum of the number of coins in the heap is not equal to 0. Then there is a move which ensures that the Nim sum of the number of coins in the heaps after your move is equal to 0.
Now suppose you are player A, so you go first. Also suppose that the Nim sum of the number of coins in the heaps is not equal to 0. Your strategy will be this: if possible always make a move that reduces the next Nim sum, the Nim sum after your move, to 0. This would then mean that whatever player B does next, by fact 1 the move would turn the next Nim sum into a number that's not 0.
Let's have a go, keeping track of the Nim sums in a table:
| Player to move next | Nim sum | Can this be reduced to 0? | Next Nim sum |
| A | not 0 | Yes | 0 |
| B | 0 | No | not 0 |
| A | not 0 | Yes | 0 |
| B | 0 | No | not 0 |
| A | not 0 | Yes | 0 |
| ... | ... | ... | ... |
This ping-pong between zero and non-zero Nim sums means that you are guaranteed a win! If player B were to win, she would have to make a move that leaves over no coins at all. That is; she would have to make a move that results in a zero Nim sum which, as we can see, is impossible. Your moves, on the other hand, always reduce the Nim sum to zero. And at some point in the game, the zero Nim sum will correspond to there actually being zero coins left — you've won.
This shows that if the Nim sum of coins in the heaps at the start of the game is not 0, then player A has a winning strategy. The strategy is to always make a move that reduces the next Nim sum to 0. (You can check that this is the strategy played by player A in the example at the beginning of this article.)
If the Nim sum of coins in the heaps at the start of the game is equal to 0, then player B has a winning strategy. Whatever player A does on the first move will result in a non-zero Nim sum when it's B's turn. And by the same reasoning as above, this means that the winning strategy is now in B's hands.
We have hidden a game of Nim in this pathway, but we have given it a different name. Can you find it? And can you implement the winning strategy?
