
When you try to work out your best move in a game, you need to think ahead. If I make this move, what are the possible moves of my opponent? And what are my possible moves in response? This gets tricky very quickly, so it can be useful to draw a picture.
To see how, let's take a very simple game as an example: you have a stack of four coins and two players take turns to take away either one or two coins. The player who takes the last coin wins.
Now look at the image below:
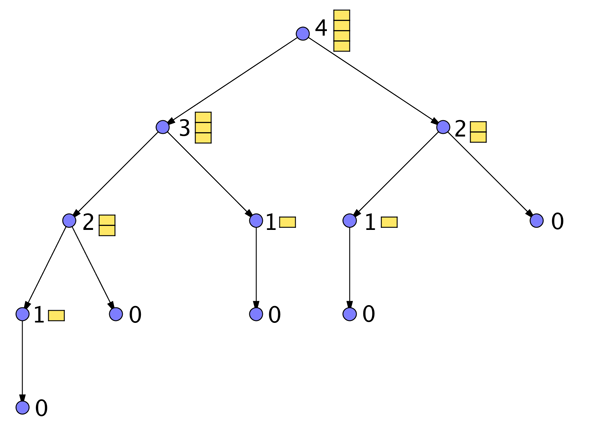
The top dot represents the beginning of the game when no coin has yet been taken. We've illustrated this by drawing a 4 beside it, and a stack of four coins. The arrows from the top dot represent all the possible moves of the first player: taking one or two coins. The two dots below represent the positions the two moves lead to: either 3 coins left, or 2 coins left. The next set of arrows represent all the possible moves of the second player from each of the positions above. And so on. A dot at the very end, labelled 0, marks an end position with 0 coins left, which in this game is also a winning position.
The picture we have created is called a game tree — and it does look a bit like an upside down tree. It is like a map of the game, describing all the ways in which a game can unfold. This particular game tree tells you immediately that the first player can be sure to win if they start by taking away one coin. Whatever the second player does in response, the first player then has a move leading to an end dot, which marks a winning position.
You can draw a game tree for any game that involves players taking turns making moves (though the labelling of the dots might be different). You can try drawing game trees for other games on this site, but be warned: they can become very complicated very quickly! Yet, they are still a useful mathematical tool for analysing games. For example, they can be used to find out whether one of the players always has a winning strategy, and what that strategy is.
