
Imagine a loop of rope. What shape should you arrange it in to enclose as large an area as possible?
To find out, let's start by forming the loop into a square. It seems that you can increase its area by bulging out the sides. If you bulge the sides out as much as you can, you will push in the corners a little, but the area you lose at the corners is much smaller than the area you gain from the bulging:
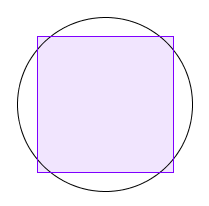
Something similar goes for all sorts of other shapes you could arrange your loop in, such as a triangle or a banana shape. If there is room for pushing the rope outwards anywhere, you can increase the area. The one shape that has no room for pushing things outward is the circle. And that's indeed the answer to our question: to enclose as much area as possible, you should arrange your loop in a circle.
According to legend, the mythical Queen Dido founded the ancient city of Carthage using this problem as a trick. Dido had to flee her home to escape from her murderous brother, and eventually ended up in the realm of King Hiarbas. She asked Hiarbas to be given as much land as could be enclosed by a single ox hide. "Sounds fair enough," the king must have thought, and granted her wish. But Dido was clever: rather than taking the ox hide as it was, she cut it into thin strips, attached them at their ends, and then laid the long strip out in a circle. This gave her an area large enough to found a kingdom on.
If you spend some time playing with a loop of rope or string, the fact that the circle is the shape that gives you the largest area becomes almost obvious. Yet, it took mathematicians a very long time to prove it. While Dido is supposed to have lived nearly 3000 years ago, a complete proof of her problem didn't arrive until 1879.
Note: Strictly speaking Dido's problem is to find a shape with a piece of straight line as part of its boundary that encloses a maximal area. The answer in this case is a semi circle.
