
Here is a 100 square board with a counter on 42:

Using either of the two operations $\times 2$ and $-5$, whereabouts on the 100 square is it possible to visit?
You might start like this: $$42, 37, 32, 27, 22, 17, 12, 7, 14, 9, 18, 13, 26, 52, 47, 42, 84 ...$$Notice that you are allowed to visit numbers more than once.
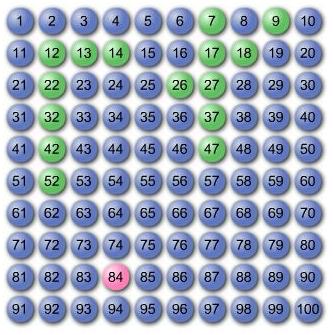
Is it possible to visit every number on the grid?
What if you start on a different number?
Can you explain your results?
Choose pairs of operations of your own and investigate what numbers can be visited.
You might like to use the interactive grid below, or print off some 100 squares.
Is there a way to predict which numbers it's possible to visit, for a given starting point and a pair of multiplication/subtraction operations?
How would your answers change if you had an infinite grid, instead of a 1-100 grid?
