
In the eighteenth century the city we now know as Kaliningrad was called Königsberg and it was part of Prussia. Like many other great cities Königsberg was divided by a river, called the Pregel. It contained two islands and there were seven bridges linking the various land masses. A famous puzzle at the time was to find a walk through the city that crossed every bridge exactly once — the path wasnt allowed to cross any bridge more than once, and it wasn't allowed to leave any bridge out. Many people claimed they had found such a walk but when asked to reproduce it no one was able to. You can have a go yourself, using the picture below.
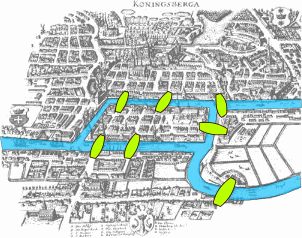
Can you find a path that crosses every bridge exactly once? Image: Bogdan Giuşcă, CC BY-SA 3.0.
In 1735 the mathematician Leonhard Euler explained why: he showed that such a walk didn't exist. Euler's solution is surprisingly simple — once you look at the problem in the right way. The trick is to get rid of all unnecessary information. It doesn't matter what path the walk takes on the various land masses. It doesn't matter what shape the land masses are, or what shape the river is, or what shape the bridges are. So you might as well represent each land mass by a dot and a bridge by a line. You don't have to be geographically accurate at all: as long as you don't disturb the connectivity of the dots, which is connected to which, you can distort your picture in any way you like without changing the problem.
The resulting picture is called a graph, made up of vertices connected by edges.

Turning the map into a graph. Image: Bogdan Giuşcă, CC BY-SA 3.0.
Once you have represented the problem in this way, its features are much easier to see. The problem of finding a path that crosses every bridge exactly once now turns into finding a path through the graph that crosses every edge exactly once.
Now let's suppose that such a path exists, and let's think of a vertex that lies somewhere in the middle of the path (that is, not at the beginning or at the end). Is it possible for such a vertex to have just one edge attached to it? Could it have three edges attached to it, or five?
What do the answers to these questions tell us about the number of edges a vertex can have? Think about this for a while, or see the answer by clicking the Reveal button.
When you arrive at the vertex via some edge, you need to leave it again by a different edge: those are the rules of the game. Therefore, any vertex that is not the starting or end-point of your walk needs to have an even number of edges attached to it: for every edge along which you enter there has to be one to leave.
What about the vertices that form the starting or end point of the walk? What can you say about the number of edges they have attached to them?
If the starting and end vertices are distinct, then they have an odd number of edges attached to them. This is because you need one edge along which to leave right at the beginning, or arrive right at the end, and an even number of edges for any other times the path visits that vertex. If the starting vertex is the same as the end vertex, then it needs to have an even number of edges attached to it.
Do these thoughts tell you why the Königsberg path is impossible?
Yes. For a walk that crosses every edge exactly once to be possible, at most two vertices can have an odd number of edges attached to them. In fact there have to be either two vertices with an odd number of edges or none at all. In the Königsberg problem, however, all vertices have an odd number of edges attached to them, so a walk that crosses every bridge is impossible.
Euler's proof marked the beginning of graph theory. He was also able to show that if a graph satisfies the condition above, that the number of vertices with an odd number of edges is either zero or two, then there will always be a path through it that crosses every edge exactly once.
The result also marked the beginning of topology, which studies shapes only in terms of their connectivity, without taking note of distances and angles. The London tube map is a great example of the topological triumph. By distorting distances and angles it turns what would otherwise be an unintelligible mess into a map that every tourist can read effortlessly. You can find out more in this article on Plus magazine.
