
How do you divide one cake between infinitely many people? Give the lucky first person (hopefully you) half the cake. Cut the remaining piece in half and give one of these pieces to the second person. Cut the remaining piece in half and give one of these pieces to the third person. And so on. Will there be enough cake for everyone? And if yes, will any cake be left over at the end?
To answer this question, imagine the cake is shaped like a square and look at this picture:
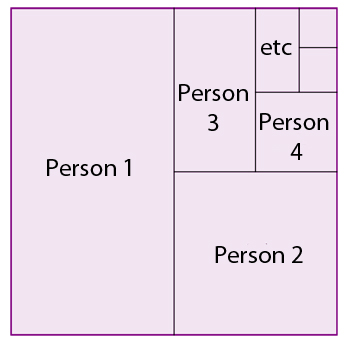
The large piece of the square, exactly half of it, is the piece that will be given to the first person. The next smaller piece, half of the remaining half, is the piece that will be given to the second person. The next smaller piece, half of half of half of the cake, is the one that will be given to the third person, and so on. You can imagine carrying on like that forever. The picture indicates that after giving out a piece of cake to a person there is always some left for the next person (you only ever give out half of what is left). It also shows that there won't be any cake left over at the end (the halving procedure will eventually fill up all of the cake) .
The picture also shows us something far more interesting. The largest piece is half of the cake. The second largest piece is half of half of the cake, in other words it's $1/2 \times 1/2 = 1/4$ of the cake. The third largest piece is half of half of half, which is $1/2 \times 1/2 \times 1/2 = 1/8$ of the cake. The fourth largest piece is half of the previous, which is $1/2 \times 1/2 \times 1/2 \times 1/2 = 1/16$ of the cake. Carrying on like this shows that the $nth$ largest piece is nth person's piece is $1/2^nth$ of the cake.
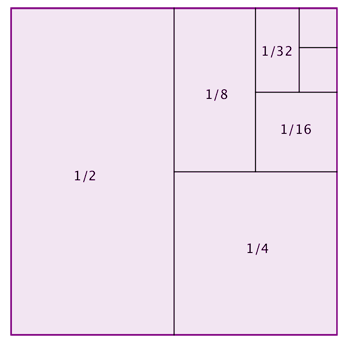
Adding all these numbers together gives a sum with infinitely many terms: $$1/2 + 1/4 + 1/8 + 1/16 + 1/32 + ....$$
As the picture shows, combining all the pieces together gives the whole cake. Therefore, $$1/2 + 1/4 + 1/8 + 1/32 + .... = 1.$$ Our picture proves that the infinite sum $1/2 + 1/4 + 1/8 + 1/16 + 1/32 + ....$ (which is called a geometric series) converges to the number 1: as we add more and more terms we get closer and closer to 1. We can get as close to 1 as we like, without ever exceeding it.
