
We saw in Folding fractions that you can fold any fraction using a method developed by Kazuo Haga, a retired biology professor from Japan. But why does this method work?
Folding a third
As before, let's start off with folding a third. Take a square piece of paper and mark half way along top side with a small crease.

Now fold the bottom left corner to meet this halfway mark and crease the paper.

The first thing to notice is an interesting relationship between the three triangles you've created, one on the top-left, one on the top-right, and one on the bottom-left overhanging the side of the paper.

At the centre of the top edge three angles fit together to make 180 degrees. One of these is a right angle (marked with a square corner in the picture), which means that the pair of other angles (marked with the single and double lines in the picture) add to 90 degrees. Each of the angles of this pair also form part of a right-angled triangle (the top-right and top-left triangles), which means the other angle of the pair also appears in each of these right-angled triangles. And the bottom-right triangle also shares an angle with the top-right triangle. And, as it is also a right-angled triangle, it too contains the same pair of angles.
This all means that the three triangles are similar – they have the same shape. That is to say, they all have the same angles, and so, have the same ratios of lengths of their sides. We can use these similar triangles, along with Pythagoras' theorem, to fold the paper in thirds.
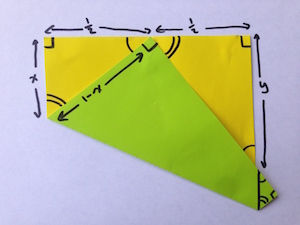
If we take the length of the side of our square paper to be 1, our top left triangle has one side of length 1/2, one side of unknown length which we'll call $x$, giving the other side a length of $1-x$. Then, by Pythagoras' theorem, we know that
$$
x^2+\frac{1}{2}^2 = (1-x)^2.
$$
Expanding this out:
$$
x^2+\frac{1}{4}=1-2x+x^2
$$
which, by rearranging, gives us $x=3/8$.
We can now calculate the length of the sides in the top-right triangle. This triangle has one side of length $1/2$ and another side of unknown length $y$. Because the triangles are similar we know that the ratio of the lengths of their sides must be the same. So
$$
\frac{y}{\frac{1}{2}} = \frac{\frac{1}{2}}{x}.
$$
And as $x=3/8$, we find that $y=2/3$. So we can construct $1/3$ by folding this length $y$ in half.

Folding any fraction
As we saw in Folding fractions, Kazuo Haga realised his method for folding a third was even more useful.
Suppose instead of folding your bottom left corner of the paper to the point halfway along the top edge, you instead fold the bottom left corner to a point a distance of $k$ along the top edge.
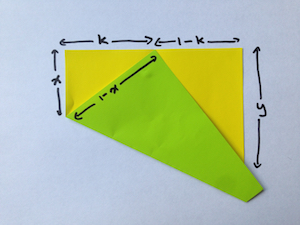
Then, the top-left triangle has sides of length $k$, $x$ and $1-x$. Then, as above, Pythagoras' theorem tells us that:
$$
x^2+k^2=(1-x)^2
$$
which rearranged gives $x=(1-k^2)/2$. And by the similar triangles argument we have that
$$
\frac{y}{1-k}=\frac{k}{x}.
$$
If we put these two equations together we find
$$
\frac{y}{1-k}=\frac{k}{(1-k^2)/2}
$$
which can be rearranged as
$$
y=\frac{2(1-k)k}{1-k^2}.
$$
And (since $1-k^2=(1-k)(1+k)$) this can be simplified to
$$
\frac{y}{2}=\frac{k}{1+k}.
$$
This is known as Haga’s Theorem and it allows us to fold any fraction we would like from a square piece of paper.


We've already seen $k=1/2$ allowed us to fold $1/3$. What if we rotate the square paper and fold the bottom left corner up to a point $1/3$ along the top edge? Then we have $k=1/3$ in Haga's Theorem which means that
$$
\frac{y}{2}= \frac{1/3}{4/3}=1/4.
$$


So far, starting from 1/2, we've used Haga's method to fold 1/3 and then 1/4. And if we carry on repeating this method we can fold any fraction. If we start with $k$ being some number $1/N$, then
$$
\frac{y}{2}=\frac{1/N}{1+1/N}=\frac{1}{N+1}.
$$
By repeating Haga’s method over and over, we can construct every unit fraction (one with 1 in the numerator): folding 1/5....


... folding 1/6....


...folding 1/7...


...and so on. And then we can use these to create any multiple of these unit fractions, and so fold any rational number. Hooray for Haga!
