Lots of Lollies | wild.maths.org

Frances and Rishi were given a bag of lollies.

They shared them out evenly and had one left over.

Just as they had finished sharing them, their friends Kishan, Hayley and Paul came along.
They wanted some lollies too so the children shared them out again between all of them.

This time they had two lollies left over.

How many lollies could there have been in the bag?

Once you've had a chance to think about it, click below to see how three different groups of pupils began working on the task.

Sarah, Danielle and Sally said:

"We noticed that $17$ works as when there are only two of them they get $8$ each, with one left over. But when their friends come along they get three each with $2$ left over.

We also noticed that $27$ works."

Poppy began like this:

If the two children end up with one lolly it must be an odd number of lollies.
Then three more children come making the total number of children $5$. Say they had $1$ lolly each when they shared them, the number of lollies would be $7$ because $1$ times $5$ is $5$ add on $2$ for the left over ones and it makes seven.

If we carry this on:

$2$ lollies each - $12$ lollies
$3$ lollies each - $17$ lollies
$4$ lollies each - $22$ lollies
...

Here is the start of Phoebe and Alice's work:

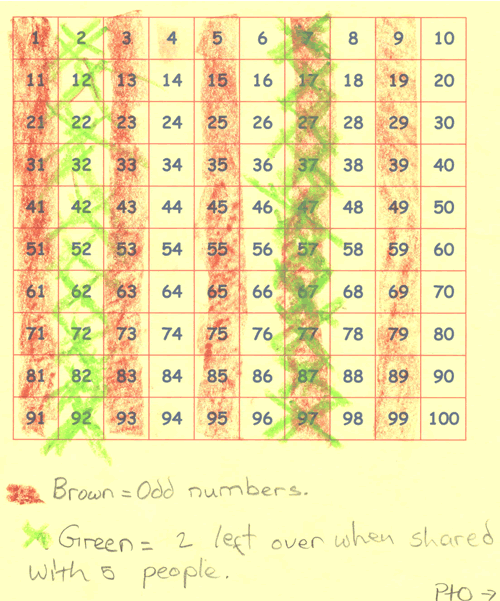
Can you take each of these starting ideas and develop it into a solution?

Extension
Here are some more "lolly" problems to explore:

A. When three children shared some lollies there was one left over. When four shared the same lollies, there was also one left over.
How many lollies might there be? What is the smallest possible answer?

What if five children shared the same lollies and found there was also one left over?
How many lollies could there be now? What is the smallest possible answer?

What if six children shared the same lollies and also found there was also one left over?
How many lollies could there be now? What is the smallest possible answer?

What if there were seven children? Or eight children?...
Is there a quick way to work out the smallest possible answer?

B. When three children shared some lollies there were two left over. When four shared the same lollies, there were three left over.
How many lollies might there be? What is the smallest possible answer?

What if five children shared the same lollies and found there were four left over?
How many lollies could there be now? What is the smallest possible answer?

What if six children shared the same lollies and also found there were five left over?
How many lollies could there be now? What is the smallest possible answer?

What if there were seven children? Or eight children?...
Is there a quick way to work out the smallest possible answer?

Comments

Lollies Problem

Permalink Submitted by Helen on Tue, 07/12/2016 - 13:26

For part B, I found that you can just find the LCM, subtract 1 and add this answer to the LCM, and it always gives the answer...ex LCM of 3, 4, 5 is 60.....60-1=59.....60+59=119 and that's the answer. Anyone knows why this works? And is there another way? Thanks

lollies

Permalink Submitted by Stephen Rhodes on Mon, 08/08/2016 - 07:47

This task links really well with "sequences"
When sharing with 2 and getting 1 remainder , this represents 2n + 1
When sharing with 5 and getting 2 remainders , this represents 5n + 2
Generate the terms for each sequence and the solutions will be those terms that are in both