
Triangular numbers can be represented by a triangular array of squares.
Here is the sixth triangular number:
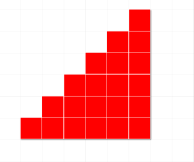
Imagine two copies of the triangular array above. Can you picture how to fit them together to make a rectangle?
What are the dimensions of your rectangle?
Can you write down the dimensions of the rectangle made from two copies of the 250th triangular number? Can you use this to work out the 250th triangular number?
Can you deduce a strategy for working out any triangular number?
Here are some triangular number relationships. Can you use diagrams to prove them?
Add together two consecutive triangular numbers. The answer is a square number.
Multiply any triangular number by eight and add one. The answer is always a square number.
Multiply any triangular number by nine and add one. The answer is always another triangular number.
Comments
The answer to the question
The dimensions of this rectangle are: 7 cm by 6cm. This means that the area is 42cm squared.
- Log in to post comments
The answer to the question
Well done! What does that mean for the dimensions of the rectangle made from the 250th triangular number? Would this help you to work out the 250th triangular number? Or any triangular number?
- Log in to post comments
the 250th triangular number
A rectangle made from two copies of a triangular number has dimensions n x (n+1)
Therefore the area made from the 250th triangular number is
When you add triangular numbers n and (n+1) the dimensions become (n+1) x (n+1) therefore it is a square number.
- Log in to post comments
the 250th triangular number
Excellent work! Could you use this value to calculate the 250th triangular number?
Could you use a picture to illustrate how the nth and (n+1)th triangular numbers add to make a square number?
- Log in to post comments
