
Imagine you have a set of 'weights' like the ones below, with two of each different weight.
You might like to think of the negative 'weights' as helium balloons...
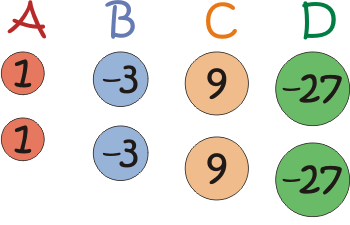
Different combinations of the weights available allow you to make different totals.
Here are some examples:
$B + 2C = 15$
$A + 2B + C = 4$
$2A + B + 2C + D = -10$
The largest total you can make is $20$. Check that you agree.
The smallest total you can make is $-60$. Again, check that you agree.
Is it possible to make all the numbers in between?
Is there a unique way of producing each total, or can you produce the same total in more than one way?
Now imagine choosing your own set of four weights (two positive and two negative), and you can have up to three of each weight.
Which set of four weights allows you to make the largest range of totals with no gaps in between?
What if you can have up to four of each weight? Or five?... Or just two?
What if all the weights were positive?
With thanks to Don Steward, whose ideas formed the basis of this problem.
