
The activities in our Geometry Journeys pathway have been inspired by the Fold and Cut problem. You can watch Dr Katie Steckles talk about this in these videos, or read on to discover even more!
The Fold and Cut problem investigates the straight-edged shapes that can be made by folding a sheet of paper flat and making a single straight cut. For example:

These problems have been around for hundreds of years. The earliest known example was published in 1721 in a Japanese book called Wakoku Chiyekurabe by Kan Chu Sen. The problem was how to cut out a sangaibisi (a typical Japanese crest) with a single cut.
Another example was reported in 1873, in Harper's New Monthly Magazine, telling how Betsy Ross recommended five pointed stars instead of six pointed stars for the American flag to George Washington, showing how she could cut one out with a single cut:









Unfortunately this story is probably not true, but it is an early published reference to this method!
Fold and cut problems were also popular among magicians in the 20th century. The five pointed star trick appears in Paper Magic, ghost written by Walter Gibson for Harry Houdini, and published in 1922. Later, the magician Gerald Loe spent some time on these problems. He could cut out any letter of the alphabet, or a circular ring of stars:

The fold and cut theorem says that any collection of straight lines can be cut in this way, that is if you have a piece of paper which can be folded any number of times and scissors which can cut through any number of layers of paper.
There are two ways to find the folds needed to do this. The “straight skeleton” method and the “disc packing” method. In theory the disc packing method always works, whilst the straight skeleton occasionally fails. However the straight skeleton method is almost always more practical in reality.
Both methods rely on two basic sorts of folds:
1. Angular bisectors: folding along the angular bisector of two lines will line them up.
2. Perpendicular folds: folding at right angles to a line will fold a section of the line back on itself.
The straight skeleton method
Here's how you use the straight skeleton method:
1. Draw the shape

2. Draw around the inside if the shape, keeping the same distance from the edges. Do the same inside the new shape, until it gets so small it disappears. Do the same around the outside until you run out of paper.

3. Draw on where the vertices go when you shrink or grow the shape in this way. This is the straight skeleton. You can see that each of the straight skeleton edges (in blue) is an angular bisector of two of the black edges.

4. From each vertex of the skeleton (blue lines only), try to draw a line out towards the neighbouring black edges, at right angles to the black edge. These are perpendicular folds. If these lines meet a straight skeleton (blue) edge they reflect through it.

5. Fold up along the red and blue lines, then cut along the black line. Sometimes it can be hard to find a way of folding it flat, but one always exists.


The disc packing method
The disc packing method involves filling the paper with circles so that each of the gaps between circles has 3 or 4 sides. Then the centres of the circles can be joined to fill the paper with quadrilaterals and triangles. This is good because it is possible to fold the edges of any triangle or quadrilateral onto each other. In the picture below, folding along the green lines will line up all the blue lines.
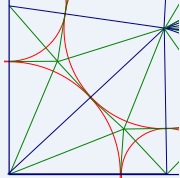
Because the lines were joining the centres of touching circles, the perpendicular folds used to do this line up nicely from one shape to the next. The problem is, the folds for this method are often too complicated to be practical.
A problem with both methods is that you might need any number of folds to be able to cut even a few cuts. Also, you might have to make a lot of folds at the same time.
References
http://courses.csail.mit.edu/6.849/fall10/lectures/L07.html
