Not the Whole Truth About Triangles

At some point in school you will have learned that the angles of a triangle always add up to 180 degrees. Always. Without exception. Whether it is an acute triangle (where all the angles are less than 90 degrees) or an obtuse triangle (one of the angles is greater than 90 degrees) triangle, a right-angled triangle, an equilateral (all sides and angles are equal), an isosceles (two sides and two angles are equal) or scalene (all sides and angles are different) triangle. No matter what it looks like, the angles of a triangle add up to 180 degrees.

Try it for yourself – draw any triangle you like on a piece of paper and measure the angles. What did you find?

Or you can try it with our interactive triangle applet - move the point to see what happens to the sum of its three angles (marked in red, green and blue).

The angles of a triangle adding up to 180 degrees feels like a fundamental truth. In fact, it was the fifth axiom of geometry the Greek mathematician Euclid came up with over 2000 years ago. You can think of an axiom as a fundamental truth. Euclid’s axioms were all the things that were possible to draw with a straight edge (a ruler with no marks) and a compass. (You can find out more about Euclid’s axioms here.)

Although we think of axioms as describing fundamental truths, that’s not quite correct. Axioms are really just rules to live by, the constraints we’ve put on our system. Euclid’s axioms covered everything that was possible to construct with a straight edge and compass: they were rules that only worked for flat spaces like a piece of paper.

So if axioms are just rules, what happens if we break them? You might be surprised to realise that you already know of lots of examples of triangles which break Euclid’s rules – triangles whose angles do not add to 180 degrees – and they are literally under your nose.

Think of a globe of the world showing the lines of longitude (they run through the North and South poles) and the equator. Then every line of longitude meets the equator at a right angle. But any two lines of longitude also meet at the North Pole, so they form a triangle with the equator. Then the sum of just two of the angles of any such triangle, those where the lines of longitude meet the equator, already adds to 180 degrees as they are both right angles. So once we add in the third angle (where the lines of longitude meet at the North Pole), we find the sum of the angles of any such triangle will always add to more than 180 degrees.

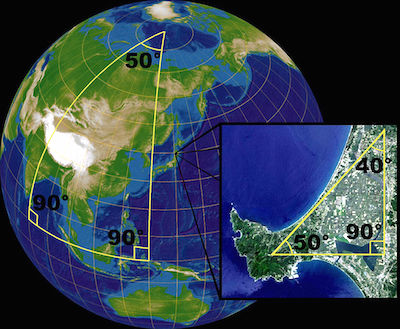
There is proof right under our feet that the angles of triangles don't always add to 180 degrees.
(Image by Lars H. Rohwedder, Sarregouset CC-By-SA)

So what is different? How can this be?

The difference is these triangles are not drawn on a flat piece of paper, they are drawn on the curved surface of the Earth. Although a small patch of the surface of the Earth looks flat, as you look at larger and larger areas of the surface you’ll quickly realise it is quite different. This is why it’s hard to draw accurate maps of the Earth on a flat piece of paper. And why you always end up with folds of extra paper if you’ve ever tried to gift wrap a football.

If you break Euclid’s triangle rule and say the angles of a triangle always add up to more than 180 degrees you get geometry on surfaces that are curved like the Earth or a ball, called spherical geometry.

You could also break Euclid’s rule for triangles in another way and say that the angles of a triangle always add up to less than 180 degrees. With this new rule we get something called hyperbolic geometry.

This geometry again happens on curved surfaces but they are curved in a different way. Hyperbolic surfaces have loads of extra material in them, so they have to curl up to fit it all in. A curly kale leaf is an example of a hyperbolic surface.

Mathematicians are really interested in geometry in all of these types of spaces: flat, spherical and hyperbolic. Physicists are too as they think the Universe we live in might not be flat after all. That’s the good thing about maths: lots of exciting things happen when you break the rules!