In the eighteenth century the city we now know as Kaliningrad was called Königsberg and it was part of Prussia. Like many other great cities Königsberg was divided by a river, called the Pregel. It contained two islands and there were seven bridges linking the various land masses. A famous puzzle at the time was to find a walk through the city that crossed every bridge exactly once. Many people claimed they had found such a walk but when asked to reproduce it no one was able to. In 1735 the mathematician Leonhard Euler explained why: he showed that such a walk didn't exist.
Euler's solution is surprisingly simple — once you look at the problem in the right way. The trick is to get rid of all unnecessary information. It doesn't matter what path the walk takes on the various land masses. It doesn't matter what shape the land masses are, or what shape the river is, or what shape the bridges are. So you might as well represent each land mass by a dot and a bridge by a line. You don't have to be geographically accurate at all: as long as you don't disturb how the dots are connected you can distort your picture in any way you like without changing the problem.

Transforming the problem. Image: Bogdan Giuşcă.
Once you have represented the problem in this way, its features are much easier to see. After playing around with it for a while you might notice the following: when you arrive at a dot via a line (enter a land mass via the bridge), then unless it is the final dot at which your walk ends, you need to leave it again, by a different line as those are the rules of the game. That is, any dot that is not the starting and end-point of your walk needs to have an even number of lines coming out of it: for every line along which you enter there has to be one to leave.
For a walk that crosses every line exactly once to be possible, at most two dots can have an odd number of lines coming out of them. In fact there have to be either two odd dots or none at all. In the former case the two correspond to the starting and end points of the walk and in the latter, the starting and end points are the same. In the Königsberg problem, however, all dots have an odd number of lines coming out of them, so a walk that crosses every bridge is impossible.
Euler also showed that if in a network the number of dots with an odd number of lines is either zero or two, then there will always be a path through it that crosses every line exactly once.
Euler's result marked the beginning of graph theory, the study of networks made of dots connected by lines. Networks are absolutely everywhere. We live in social networks, travel along road and rail networks, and rely on telephone networks and utility networks that deliver power or water. Our computers and phones are hooked up to that vast network called the internet. Graph theory, started by Euler nearly 300 years ago, is needed to understand all of these networks.
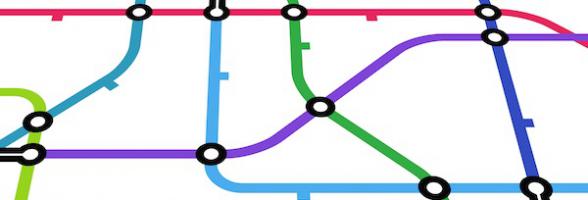
The result also marked the beginning of topology, which studies shapes only in terms of their connectivity, without taking note of distances and angles. The London tube map is a great example of the topological triumph. By distorting distances and angles it turns what would otherwise be an unintelligible mess into a map that every tourist can read effortlessly.
Leonhard Euler (1707-1783) was one of the greatest mathematicians of all time. He wrote more than 500 books and papers during his lifetime — about 800 pages per year — with an incredible 400 further publications appearing after his death. His collected works and correspondence are still not completely published: they already fill over seventy large volumes, comprising tens of thousands of pages.
Euler worked in an astonishing variety of areas, ranging from the theory of numbers, the geometry of a circle and musical harmony to calculus, mechanics, optics, astronomy, the motion of the Moon, the sailing of ships, and much else besides. Solving the Königsberg problem was just small part of his vast body of work.
Further reading
You can find out more about Leonhard Euler, the Bridges of Königsberg problem, and the London Underground map in the following articles on Plus magazine (which are slightly more advanced):
