The story of George Boole is an extraordinary example of collaboration across the centuries. George’s work provided the foundations for building today’s computers and mobile phones, yet George died many years before the first computers were invented. How did a mathematician who lived, and died, in the nineteenth century have such an impact on our twenty-first century technology? This is the tale of self-taught mathematician George Boole and the modern day engineers who recognised the power of his ideas.
George Boole’s early life did not mark him out as a ground-breaking mathematician. Born in 1815, he was the son of a local cobbler and would have been expected to work in the family shoe making business when he grew up. But his father’s business collapsed and George became a school teacher instead. He spent his evenings and weekends exploring his mathematical ideas, attracting the attention of the world famous Royal Society and later becoming a Professor of Mathematics.
As a professor, George could study mathematics full-time. His most famous work brought together logic and algebra. George’s breakthrough was developing a new type of algebra for statements that were either true or false.

George Boole (1815 - 1864).
For example, ‘David Beckham is a footballer’ and ‘Quidditch is an Olympic sport’ are two statements. We know that one of them is true and the other is false (I’ll let you decide which is which!). Let's write A for the statement 'David Beckham is a footballer' and B for 'Quidditch is an Olympic sport'. Then what about the statement A AND B: ‘David Beckham is a footballer AND Quidditch is an Olympic sport’? It's clearly false! For it to be true, we would need each of A and B to be true, which isn't the case. Therefore, the statement A AND B is false. If we assign the truth value 0 to a false statement and the value 1 to a true one, then we can write the AND connective as a kind of multiplication: A x B stands for A AND B, and since one is true and the other false, we see that A x B has the truth value 0 x 1 = 0.
What about the statement A OR B? 'David Beckham is a footballer OR Quidditch is an Olympic sport'? For this to be true only one of A or B needs to be true, which is the case in our example. Hence A OR B has a truth value of 1. We can write it as a kind of addition: A + B stands for A OR B, and since one is true and the other false, we see that A + B has the truth value 0 + 1 = 1.
Using these ideas George built a whole system of logic, which allows you to decide if a statement is true or false, using Boolean multiplication and addition. The following two tables show the truth values of A AND B and A OR B for all the possible combinations of truth values of A and B. They also show the associated arithmetic. The only thing that is different from the arithmetic we are used to is that in Boole's addition 1 + 1 = 1.
|
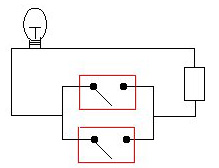
Boole and computersHave you noticed that we only needed to use two digits, 1 and 0? George's ideas became very interesting for electrical engineers long after his death: they made it possible to build the central processing units (CPUs) in our modern day computers. Computers represent all the information they store as strings as 0s and 1s. When they complete a task, such as updating your Facebook status, they need to manipulate these strings according to logical rules. To see how to get logic into a computer, think of an electrical circuit with two switches and a light bulb:
The light bulb comes on if the circuit is closed, otherwise it remains off. Looking at the picture, you see that the light bulb comes on if either or both the two switches are closed. Now think back to our Beckham and Quidditch statements. If either or both of the statements A and B are true, then A OR B is true. We can show both situations using a table. We write 1 for a switch being closed, 0 for a switch being open, and 1 for the light being on and 0 for the light being off:
|