
Choose a starting number from a 1-100 square and cross it out.
Then choose a factor or multiple of that number.
Keep crossing out factors or multiples of the last number in the chain.
For example, Charlie started with 60, 30, 6, 96, 16, 32, 8, 56, 7, 21, 42,...
What's the longest chain you can make?
You may wish to download a 1-100 square to work on, or you could use the interactivity below.
Comments
Maths
I really enjoy ... still learning and understanding how it goes.
- Log in to post comments
Beware the Primes
Through trial and error with 7th grade students (13 years old) we have found that 74 is the maximum chain that can be made.
We are still thinking, but we believe that the reason has to do with the 26 primes in between 1 and 100 (100-26 = 74).
- Log in to post comments
one and a prime
Yes - if you've linked all you can, except for the 1, you can link that to a prime number.
- Log in to post comments
Maximum Chain Length
I am almost certain the maximum chain is between 77 and 78 because I have made a chain that is 77 numbers long.
My chain is:
I think it may be possible to produce a chain of 78 because I found a pattern that is consistent and it predicted a length of 78 however I spent a lot of time rearranging the chain and I still haven't found a way to make it 78 long.
- Log in to post comments
Maximum Chain Length
That's a very impressive chain, well done!
You mentioned a consistent pattern that you found, could you explain what that pattern is?
- Log in to post comments
Bigger Square
My longest chain is 41 numbers! I don't know any more combinations there are for it because I've forgotten how I did my chain! OOOPS!!! Silly me! I'm thinking of doing it again with number 1-121 on an 11 x 11 grid! Do you think I have a good idea for expanding minds?
- Log in to post comments
Bigger Square RESULTS
My chain is:
41 numbers altogether!
Hey, I've got two questions that will put your brain in gear!
1. What do all the 41 numbers make when all added up?
2. What do all the DIGITS added up make? Share your answers!
- Log in to post comments
Chains
We got all the numbers. Has anyone else?
- Log in to post comments
Our longest chain
We are Year 5 and our longest chain is 51. We started on 99.
- Log in to post comments
34!
Here is my chain:
96 and 64 had the most prime factors so I worked on both sides of the chain until I was stuck and connected them both with a 1. I made sure that there were no duplicates.
- Log in to post comments
74!
I think this may be right
I need just 3 more do you guys have any idea of what numbers could be added to make 74?
I did this at school and got the best in the class any help ??????????
- Log in to post comments
Primes failure
The problem I see with getting a complete chain is the primes, of course. More importantly, the primes over 50.
If you start your chain with 53, the next multiple is 106, too high, so you have to find a factor. The only factor is 1. The same is true for all the primes above 50. At most you can use one of them in your chain, at one end.
For any N, you can only have one prime larger than (N/2) in your chain.
examples
N=1: 1
N=2: 1, 2
N=3: 3,1, 2
N=4: 4, 2, 1, 3
N=5: oops, can't use both 3 and 5. Max is chain of 4 numbers 5, 1, 2, 4 or 3, 1, 2, 4
N=6: 4, 2, 6, 3, 1, 5
N=7: can't use both 5 and 7. Max is chain of 5 numbers.
There are 10 primes above 50 ( 53, 59, 61, 67, 71, 73, 79, 83, 89, 97) so there is an absolute max chain length of 91 (100-10+1). I doubt that can actually be achieved though.
There is probably a similar problem with the primes between N/2 and N/3, being also limited in usage (like you can only use 2 or 3 of them, max), but I haven't given it much thought yet.
- Log in to post comments
36 is our highest yet!
We did:
- Log in to post comments
63!
I got 63! It was really challenging getting from about 57 to 63. Had to get out the pencil and paper. I don't know if I can go higher right now.
- Log in to post comments
Chains
I love this activity, but wish solutions were not posted where students can so obviously see them as it discourages them from thinking themselves, but just copying. Could the interactive be posted elsewhere for students to use with no solutions shown?
Thanks
- Log in to post comments

Here it is!
Hi Mike, you can access the interactive on its own without comments here: https://nrich.maths.org/factmult/ Hope that helps!
- Log in to post comments
Thanks so much! Great
Thanks so much! Great activity
- Log in to post comments
46, Hoping to improve still!
I have successfully made it to 46 and have done this starting at 100 and then I have divided then I have multiplied numbers to try to get the order.
The order of the numbers are
- Log in to post comments
i got 73!!!
Here´s my chain:
That´s it! please feel free to show to your parents or kids, siblings, and family! Also feel free to copy too! Have fun trying to beat me!
Also can you guys tell me how to get a scale higher than 100?!
Thanks and have fun!
- Log in to post comments
Not quite 73
That's an excellent chain, but I'm afraid you've made a few errors. I've hidden them below in case you want to find them yourself:
- At "69, 31, 62, 1", 31 isn't a factor of 69. However, if you remove 31 and 62 from there, then that fixes the gap in your chain.
- At the end, 76 is not a factor or multiple of 68, nor are 19 or 57. However, if you put 2 between 68 and 76, then you can connect them.
- You could also put 3 at the end to add another number and then perhaps another multiple of 3.
With these changes, you could make a chain of 70.
As for a scale larger than 100, I'm afraid the interactivity only supports a 1-100 square. However, you could make a different grid of your own using a spreadsheet.
- Log in to post comments
Factors and Multiples Longest Chain
After one day trial the longest chain I got was 66:
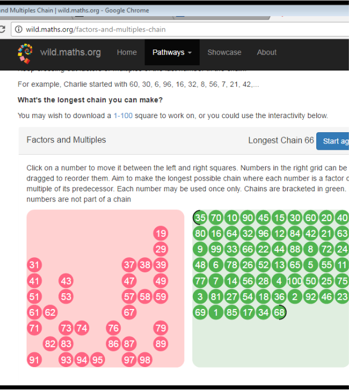
If anyone has a longer chain please do share it!
Thank you
- Log in to post comments
Factors and Multiples Longest Chain
That is an excellent chain. Would it be possible to make it longer by inserting some numbers in between existing parts of your chain? For example, you could make it a little longer by inserting 98 between 7 and 14
- Log in to post comments
Chain of 73
Year 6 pupil proud of achieving a chain of 73. A proud teacher too :)
- Log in to post comments
Chain of 73
That's a very long chain. Could you list the numbers in your chain? Or alternatively, could you send us a screenshot of your number chain in the interactivity?
- Log in to post comments
77 my best yet
Here is my chain:
- Log in to post comments
Factors and Multiples Chains from different groups.
Year 5/6
Some children found chains of 24 by finding multiples then factors and repeating this.
Some children found chains of 36 through just randomly finding factors and multiplying and working through the process of elimination.
Thoughts:
If you just multiply you get a smaller chain even if you start with a smaller number.
Some children started multiplying then finding factor and repeating, creating a longer chain.
They think that by looking at more chains next time they will be able to find a pattern.
- Log in to post comments
