
We start with any four numbers (not zero!)
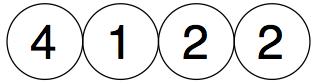
We then add in pairs and place the totals above them :-
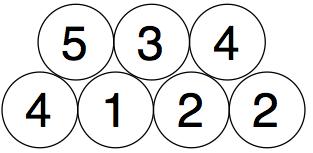
And we then add in pairs the new numbers we just got.
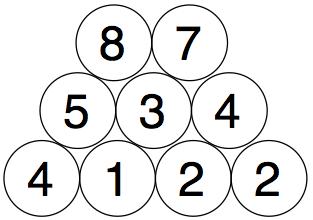
We do the same with those two numbers to get our final number.
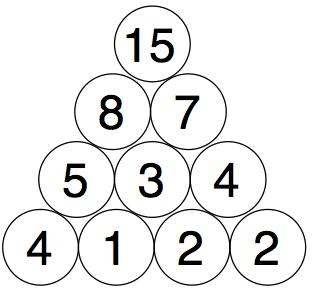
You need to find four starting numbers to place at the bottom so that when you get to the top it's 15 each time.
Try to find as many starting four numbers as you can.
Think about good ways to do this. Maybe use a system!
What little change can you make to the rules to explore again?
What new ideas can you think of to make this different? Explore those!
Here is a brand new variation that has lots and lots within it to explore - There are no longer four numbers at the bottom, but seven and they are 1, 2, 4, 8, 16, 32, 64. Build it up in the same way as before and when you've reached the top, explore and create other versions.
Comments
Problem
This is impossible!
- Log in to post comments
Solution Help
If you are struggling then this may help you get started (Answers not included)
Work from the top to the bottom (start with 15, find two numbers that add up to 15. e.g 10+5)
Then carry on descending until you have your SUPER SOLUTION!!!
We really hope we helped!
- Log in to post comments
no its not
HOW is this impossible?
- Log in to post comments
Math
Its not impossible you just need to have two 1s and two other numbers 1-10
- Log in to post comments
Keep trying!
What have you done so far? It would be good to know what you have tried so we can try to help.
- Log in to post comments
build it up
We started at the top and worked down and you can only use 1 at the bottom.
15
96
542
2311 That is our method.
- Log in to post comments
Well done, Elliott and Toby!
Well done, Elliott and Toby! Can you find any other solutions with 15 at the top?
- Log in to post comments
How many possible combinations are there?
I have 4 so far- how many ways can you make 15
- Log in to post comments
There are an infinite number of solutions
Say the numbers on the bottom row are a, b, c, and d respectively. The numbers on the second row will thus be a + b, b + c, and c + d. The numbers on the third row are a + 2b + c and b + 2c + d, and finally, the numbers on the top row are a + 3b + 3c + d. Thus, all one needs to do is to find nonzero solutions to the equation a + 3b + 3c + d = 15, of which there are infinitely many solutions.
- Log in to post comments
Some Examples
- Log in to post comments
Restricting to positive integers
I've used reveal here so that those who want to work on it on their own will not instantly see a solution without pressing "reveal".
- Log in to post comments
We loved this!
We loved this!
Stingrays class spent twenty minutes in competition with each other to create pyramids that added to fifteen. We double checked them all and we found 18 solutions!!
A great puzzle we really enjoyed.
- Log in to post comments
We think there are more than 18
We started at the top and found out that is the smallest left hand number in row 2 (as you can't have 1 in any row except the bottom)
Increasing by one eactime we think there are 12 and then each of those can be done in reverse (read right to left) to make 24 total
- Log in to post comments
Our solution
I've used "Reveal" here because this solution uses Mathematics that many under 14 year olds will probably not have come across and may find off-putting.
- Log in to post comments
Whoops
We just found another one
- Log in to post comments
can you use negative numbers
if you can use negative numbers please say because if you can it will open up a lot of new answers
- Log in to post comments
awesome
simple to learn but hard to master. There are a few ways to make 15 that I worked out but once I thought that there was no more ways to make 15 I cheated a bit because I put 15 at the top and worked from there. If you are struggling 3213
- Log in to post comments
Complicated Addition or Subtraction - Making a Pyramid
Many of us started at the top and worked our way down by breaking down the numbers until we got to the bottom row. There are LOTs of solutions for example
15
9 6
5 4 2
2 3 1 1
- Log in to post comments
My method
work from the top down
- Log in to post comments
another method
15
7 8
3 4 4
2 1 3 1
- Log in to post comments
more methods
15
9 6
6 3 3
4 2 1 2
- Log in to post comments
A Method That May Not Be Helpful
- Log in to post comments
Whole number solution
We used only whole numbers. You cannot have an infinite number of solutions. The numbers 1, 2 and 3 cannot appear in the second row otherwise 1 will appear in the third row and you can't have 0 in the bottom row. 'There always has to be a 1 in the bottom row. If you have 4122 you can't count 2214 as it is just the same numbers but backwards. We found 11 solutions: 4122, 2131, 1118, 2221, 5211, 4115, 1132, 7112, 3116, 4212 and 3123.
- Log in to post comments
There is twelve
Ther is twelve ways to make it
- Log in to post comments
What age is this appropriate for?
will a year 1 student be able to solve this, i mean finding an alternate combination to get 15 on the top
- Log in to post comments
Maths Build It Up Problem
Our class found 23 solutions to the problem! We worked hard to swap numbers around and we used a lot of trial and error. The children did not start at the top and tackled this problem bravely and with perseverance. I am very proud :)
- Log in to post comments
Only certain numbers work.
- Log in to post comments
BUILD UP
- Log in to post comments
Number of solutions
Hello,
How many solutions did you find when you used different digits on the bottom row? We currently have 9 different sets of numbers on the bottom row!
- Log in to post comments
Build it up
Can you put ten in?
- Log in to post comments
maths
if you take four numbers like 4,1,2,2 you can make lots of build up
- Log in to post comments
Build it up
- Log in to post comments
We're proud of ourselves!
Hello World! :)
We are the students of Room 11. A Year 4 classroom in Waterlea Primary School, in Auckland, New Zealand. Early on in the challenge, we found that starting from the top made it easier. We then tried many combinations of numbers and had 40 different solutions! Our teacher showed us that we had a few solutions that had doubled up, so we removed them. Then, we double-checked our answers and found that some were incorrect! Finally, we ended 22 different solutions. We are all very proud of the effort we put in!
- Log in to post comments
I know it!!!!
- Log in to post comments
